遗传算法最初由美国密歇根大学的 J.Holland 提出,是一种通过模拟自然界生物进化的过程来搜索最优解的算法,应用于量子计算、电子设计、游戏比赛等多种场景。
以大家熟知的 python gplearn 为例,它就是一款基于遗传算法开发的数据分析工具,它可以自动生成计算公式、优化特征选择和因子的非线性表达式,为因子挖掘提供了一种新的选择。
但随着量化投研需求的不断升级,gplearn 的局限性逐渐显现。遗传算法需要对大量复杂公式计算适应度,而 gplearn 的性能瓶颈导致因子挖掘的效率偏低。此外,gplearn 只支持从二维数据中提取特征,这使它并不适用于金融领域中对时间、标的和特征构成的三维数据进行挖掘的场景。
对此,DolphinDB 推出了 Shark GPLearn。
相较 gplearn,DolphinDB 的 Shark GPLearn 在性能上可实现近百倍提升。而且,Shark GPLearn 具有更丰富的算子库,并提供了高效的 GPU 版本实现。它引入分组语义,可以在训练中分组计算,从而支持在三维数据中挖掘因子。为了充分发挥 GPU 性能, Shark GPLearn 还支持单机多卡进行遗传因子挖掘,进一步提升效率和规模。
接下来,我们将以基于股票日频 K 线数据的因子挖掘为例,展示如何使用 Shark GPLearn 进行因子挖掘。(完整案例及代码展示可前往 DolphinDB 官网【开发者中心】-【白皮书】获取)

基于股票日频 K 线数据进行因子挖掘
第一步:导入数据并进行预处理
本例中,我们选取 2020 年 8 月 12 日至 2023 年 6 月 19 日期间的股票日频 K 数据,计算收益率、个股 20 个交易日后的收益率等训练相关指标。导入后对数据进行【选取”0“、”3“、”6“开头的 A 股数据】、【获取基础指标】、【计算收益率和 52 周最高价/最低价】、【删除空值】、【选取每天都有数据的股票】等预处理。
第二步:训练模型
在这一环节中,我们按【拆分训练集和测试集】→【获取训练集】→【配置算子库】→【创建 GPLearnEngine 引擎】→【自定义适应度函数】→【挖掘因子】的顺序进行模型训练。
首先,我们将前 80% 的日期数据作为训练集,剩下 20% 作为测试集,通过 sql 函数查询指定列(xCols)作为模型输入数据。
接着,创建 createGPLearnEngine 引擎,初始化遗传算法模型,设置种群大小、进化代数等参数,并指定算子库(如滑动窗口函数)。本例中,我们通过spearmanr、groupby、mean 三个函数实现因子 rankIC 的计算逻辑,生成一个自定义适应度函数。
最后,调用 gpFit(50) 进行训练,挑选出最优的 50 个因子。本次测试数据集约 166W 行,训练 50 个因子的耗时约 9 秒,挖掘出的因子公式如下:
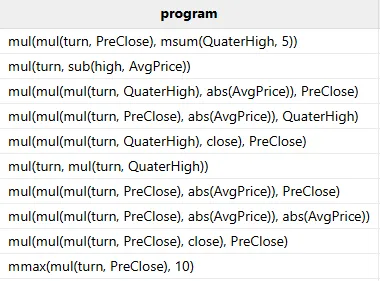
第三步:因子评价
尽管 Shark GPLearn 可以快速挖掘出大量因子公式,但并非所有因子都有效。因此,在正式使用因子前,需要进行单因子评价、多因子回测等步骤。
在因子评价环节,DolphinDB 自主开发了 Alphalens 模块,其开发逻辑与 Quantopian 用 Python 开发的 Alphalens 相同。通过 Alphalens 模块,我们可以计算出不同持仓周期下的因子 IC 值序列。
本例中,我们使用 IC 值分析法进行简单的因子评价,按序进行以下操作:【计算单因子】→【单因子分析】→【获取每日收盘价】→【调用自定义函数对批量获得的因子进行 IC 值分析】。
首先,使用 calFactor 函数,通过 parseExpr 函数将表示公式的字符串转化为元代码;再使用 sql 函数,动态生成 sql 语句;最后通过 eval 函数执行元代码,获得对应公式的因子值。
接着,通过调用 Alphalens 模块中的 get_clean_factor_and_forward_returns 函数进行数据处理获得单因子分析中间结果;再调用 create_information_tear_sheet 函数计算因子的 IC 值。我们可以调用 peach 函数将 single_factor_analysis 应用到所有因子公式上,快速处理大量因子。
本例将 IC 值大于 0.03 且 IR 值大于 0.5 的单因子视为有效,并对其进行多因子回测。挖出的第一个因子的 IC 值为:

第四步:模型优化
为更快挖掘出有效因子,需要对模型进行反复的调参尝试。
本例中,我们针对进化轮次、节俭系数、初始化公式等参数进行详细的对比实验。
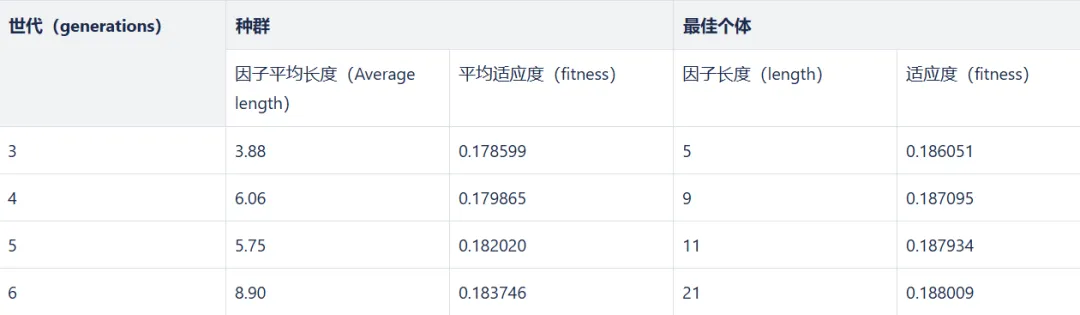
从这张进化轮次和因子适应度以及长度的关系表中可以看出,迭代次数越多,适应度越高,但增长幅度有限;迭代次数越多,因子长度越长,公式复杂度增高,失去可解释性。
对于节俭系数,我们希望最大化优化目标,且公式不要过长,所以仅测试 generations=6 时 parsimonyCoefficient ≤ 0 的情况。测试结果如下:
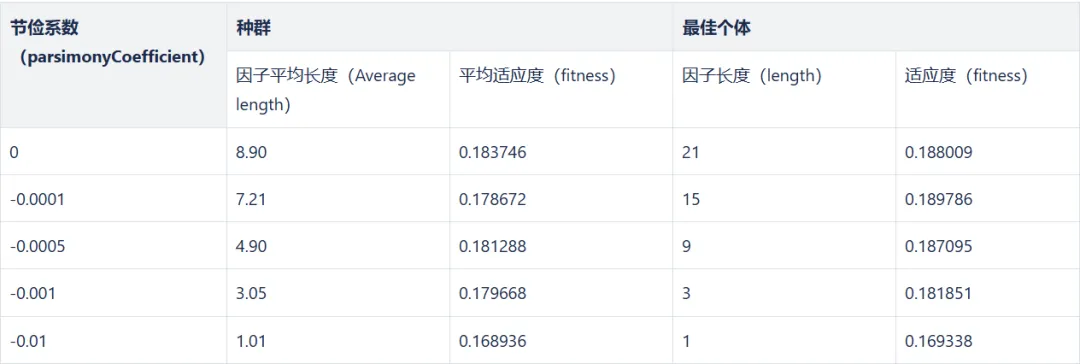
从这张节俭系数和因子适应度以及长度的关系表中可以看出,节俭系数的绝对值越大,公式长度对适应度的影响越大。当设置过大时,长度影响甚至超过 fitness 函数的影响,不利于挖掘有效的因子。
同时,由于 Shark GPLearn 支持设置初始化公式,所以用户可以基于已知的有效因子进行进化和变异,减少初始公式的随机性,更有目标地进行因子挖掘。
本例中,我们从国泰君安 191 因子库中选取 70 号因子作为初始公式进行优化,输出的第一个因子的 IC 值如下:

我们发现,虽然相较一开始的因子,样本内 IC 值有所提升,但因为初始公式只有一个,生成的因子组成单一。对此,我们可以通过增加初始化公式和调节 size(initProgram) \ populationSize 的比例、让初始种群里加入随机生成的公式这两种方式丰富初始化种群。
于是,我们将初始化公式由 1 个增加到 8 个,同时,在初代种群的 1000 个个体中,500 个由指定的初始化公式生成,其余的随机生成。经过筛选,表现较好的因子如下所示:
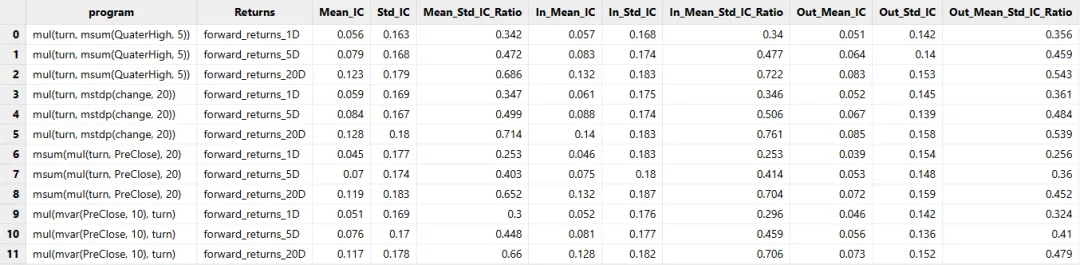
以上就是使用 Shark GPLearn 进行自动因子挖掘的简单示例。如果想了解更多 Shark GPLearn 架构实现、功能特性等信息,欢迎访问官网获取 Shark GPLearn 高性能因子挖掘白皮书,并下载试用 DolphinDB~