绵烁资产:基于 DolphinDB 构建因子收益模型
业务背景
作为深耕量化投资领域的专业机构,绵烁资产始终致力于提升组合风险收益比的精细化测算能力。面对A股市场风格切换频繁、因子有效性动态变化的挑战,原有基于传统回归框架的多因子模型在行业敞口控制与特质收益分离方面逐渐显现瓶颈。为此,绵烁资产引入DolphinDB数据库,结合多因子风险模型框架,构建新一代因子收益预测与风险管理体系。
技术实施路径
- 因子计算与标准化
基于DolphinDB分布式计算引擎,实现126个三级因子的批量化处理。通过MAD去极值法消除异常值干扰,采用市值中性化处理消除规模效应。例如对盈利质量因子(Earnings Quality)进行标准化. - 因子有效性动态评估通过滚动窗口计算因子稳定性系数(FSC)与信息系数(IC)。针对动量因子(Momentum)的月频FSC监测显示,其稳定性始终维持在0.85以上;而部分成长因子在2023年期间的IC值呈现周期性波动,触发动态权重调整机制。
- 多因子合成与模型构建采用IC-IR加权方法,将三级因子合成8个一级风格因子。通过DolphinDB内置的加权最小二乘(WLS)回归,构建截面收益预测模型。
核心技术创新
- 风险矩阵优化:引入Newey-West调整消除因子收益自相关性,通过贝叶斯收缩技术压缩特质收益协方差矩阵的估计误差。实测显示,经调整后的组合波动率预测偏差较传统方法显著收敛。
- 动态行业中性控制:在组合优化模块嵌入申万行业约束条件,确保投资组合相对基准的行业偏离度控制在±2%以内,有效降低风格漂移风险。
基于 DolphinDB 的收益风险模型
在本例中,用户使用 DolphinDB 模型部分构建因子收益模型。
以下为一个示例:通过 moving wls 多因子回归模型,函数接口为 getAllFactorValidate。
/* getAllFactorValidate
获取moving wls多因子回归结果统计量的聚合函数
Input: y 因变量
x 自变量
w 权重
Output:
wls stat "beta","tstat","R2","AdjustedR2","Residual" */在构建得到多因子风险回归模型后,再基于 getRetTable 函数计算如下模型评估指标:
- stR2:该值为多因子风险模型中定义的 R_2 ,计算方法为:
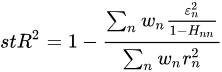
其中 rn 为个股 n 的超额收益, εn 为截面回归的残差, wn 是个股的加权权重, Hnn 为 H=X(X′X)−1X′ 的第 n 个对角元, X 是因子暴露矩阵。
2. t 检验:该值为标准的 t 统计量,用来衡量回归系数的统计显著性。
3. 偏差统计量(bias_statistic):该统计量是一种通用的衡量模型预测程度的统计量,直观来看,该统计量计算的是实际的风险比上预测的风险。令 Rnt 为组合 n 在 t 时刻的收益率, σnt 是 t 时刻的波动率预测。计算方法为:令 bnt=Rntσnt ,可理解为对 Rnt 的波动率进行标准化,则预测准确则 bnt 的标准差为 1。组合 n 在 t 时刻的偏差统计量为:
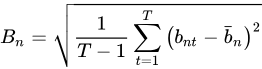
其中 T 是总截面时间数。当收益率符合正态分布的假设下,偏差统计量 Bn 的 95% 置信区间为:
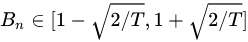
因此当观测发现 Bn 接近 1 时,则可以初步推断模型的预测值是比较准确的。
4. Q 统计量(Q_statistic):基于偏差统计量中计算的 bnt ,该统计量惩罚了欠拟合或者过拟合的情况,Q 统计量的计算方法为:
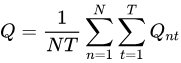
风险调整
在构建得到多因子风险回归模型后,若要求解多因子风险模型中的个股收益率协方差矩阵,则需要分别求解因子收益率协方差矩阵 Vf 、特质收益协方差矩阵 Δ 。然而基于样本求解得到的 Vf 、 Δ 估计结果都是有偏的,因此需要分别对因子收益率风险矩阵、特质收益协方差矩阵分别进行协方差调整。
因子收益率风险调整
Newey_West 调整Delta
多因子风险模型必须进行 Newey-West 协方差调整的原因主要有以下两点:
- 多因子风险模型是日频的,然而风险预测模型是月频的,因此需要对日频的协方差矩阵通过尺度变化,转化成月频的协方差矩阵,而这个过程必须考虑日频因子收益率的自相关性。
- 实际应用中,基于多因子风险模型预测的因子收益率往往存在时序相关性。此时样本风险矩阵并不是真实收益率风险矩阵的相合估计(随着样本数增加,相合估计会收敛于真实值,这有助于计算估计量的估计误差),因此需要调整由计算出来的日收益率存在 q 阶序列性导致因子收益率的风险矩阵 Vf 。
本文 Newey-West 协方差调整的接口为 Newye_West 函数,在 getRetTable 函数的 adjust=true 时调用。
/* Newye_West
Newye_West调整得到协方差矩阵
Input:
ret 收益率表
q 收益率自相关阶数
Output:
cov Newye_West调整后的协方差阵
*/
上述接口主要实现步骤如下:
- 步骤一,假设 Ft 可满足 MA(q) 过程,则可先基于移动平均过程进行简单校验,如下:
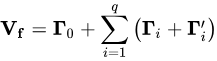
其中
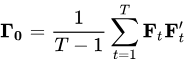
为不考虑自相关性的样本协方差矩阵;
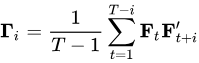
代表着由当期的收益率向量以及滞后i期的收益率向量所得到的自协方差矩阵,但 Γi 本身并不对称,因此对于任何的滞后期 i,都需要 Γi和 Γi′ 成对出现。
- 步骤二,对 Γi的修正加入 Bartlett 权重系数 wi=1−i1+q ,该系数与滞后期成反比,若收益率向量间的滞后期越长,则赋予 Γi的权重则越小。经过证明可以发现,该修正后所得到的样本风险矩阵 Vf 是真实的风险矩阵的相合估计,且是半正定矩阵。
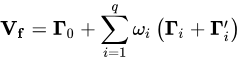
Eigenfactor 调整
令Vf 是 K×K 的因子协方差矩阵,利用特征分解,可以将 Vf 写成对角形式 D0=U0′VfU0 ,其中 U0 是Vf 中相应特征值的特征向量组成的特征向量旋转矩阵。业务上来说,假设有 N 支股票,则 U0 的每一列都是一个特征因子投资组合权重(N*1 维),以该权重构建得到 eigenfactor portfolio(特征因子投资组合,来自特征向量 eigenvector),其中 D0 的每一个对角元则是相应的 eigenfactor portfolio 的波动风险。eigenfactor portfolio 在构建投资组合的最优化构建中有很大的意义:
- eigenfactor 之间彼此独立,两两之间的协方差为零。
- 方差最小的 eigenfactor 代表以最小化组合方差为目标函数实现的组合,而方差最大的 eigenfactor 代表以最大化组合方差为目标函数实现的组合。
然而若直接特征分解会存在偏差,其中风险越小的 eigenfactor portfolio 的偏差反而较大,因此需要进行 Eigenfactor 调整。本文 Eigenfactor 调整对应的接口为 eigenCovAdjusted 函数,在 getRetTable 函数中当参数 eigenfactor=true 时被调用。
/* eigenCovAdjusted
eigenCovAdjusted调整风格因子协方差
Input:
cov 因子收益率协方差阵
M 蒙特卡罗模拟:重采样次数
Output:
cov eigenCovAdjusted调整后的协方差阵
*/上述接口的主要实现步骤如下:
- 步骤一,首先基于蒙特卡洛模拟构造出相对于“真实值”的具有偏差的协方差矩阵 Dm=Um′VmUm ,即”模拟协方差矩阵“。
- 生成服从均值为 0,协方差为 D0 的 K×T 维的多元正态因子收益 bm ,每一行代表一个 eigenfactor 的收益率序列。因此 fm=U0bm 代表了原因子的模拟的收益时间序列,其对应的协方差矩阵 Vm=fmfm′T−1 即为得到的模拟协方差矩阵。
- 进一步特征分解,即可得到模拟的 eigenfactor 的协方差矩阵 Dm=Um′VmUm 。
- 步骤二,以上模拟的 eigenfactor Um 实际上是以样本协方差矩阵 Vf 作为真实的因子收益率协方差矩阵的得到的,其中 Vf 可以理解为 Vm 的真实值,Vm 是 Vf 的无偏估计;因此模拟的”真实协方差矩阵“为 D~m=Um′V0Um 。
- 步骤三,计算缩放量/偏差调整系数。由以上得到的 Dm 和 D~m 的对角元的 Dm(k) 和 D~m(k) ,可以计算得到偏差调整系数:
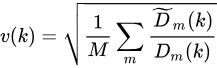
其中 M 为 Bootstrap 模拟总次数。
- 步骤四,调整基于样本计算得到的 eigenfactor矩阵 D0:D~0=v2D0 ,其中 v 是由 v(k) 生成的对角矩阵,最终可以给出经过调整后的协方差矩阵为 V~f=U0D~0U0′ 。
基于贝叶斯收缩的个股特异性收益率风险调整
贝叶斯收缩(Bayesian Shrinkage)是一个常见的将先验和样本估计值结合起来的手段。
本文的贝叶斯收缩的接口为 BayesShrinkage 函数,在 getRetTable 函数中当参数 shrink=true 时被调用。
/* BayesShrinkage
BayesShrinkage调整特质波动率
Input:
cov 特质收益率协方差阵
weight 市值权重
q λ_F 压缩系数
Output:
cov BayesShrinkage调整后的协方差阵
*/上述接口的实现步骤如下:
- 步骤一,计算样本估计值——基于 WLS 预测得到的特异性收益的风险 σn 。
- 步骤二,计算先验值——首先选择与目标个股处在同一市值的所有股票,再基于市值加权计算的特异性收益率的波动的平均值。
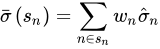
其中多因子风险模型把所有个股按照市值分成十档, sn 表示对应的市值档位, σn 为同处在 sn 市值档位下的n支股票的特异性收益率的波动, wn 表示 n 支股票按照市值计算的权重。
- 步骤三,贝叶斯收缩(使样本估计值向先验靠拢),计算后验估计。
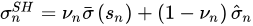
vn 是在收缩时赋予先验的权重(称为收缩强度系数),具体公式如下:
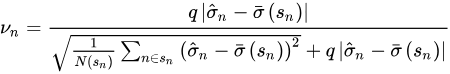
其中 N(sn) 是当前个股市值档位中的个股总数;
|σn−σ¯(sn)| 为样本特异性波动率与先验的偏离程度;
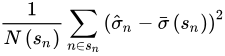
为 sn 市值档位下样本特异性波动率与先验的偏离程度的标准差, q 为经验压缩系数,其意义在于更偏重组内的标准差还是更偏重股票相对组内均值的偏差。当 |σn−σ¯(sn)| 越高,即目标股票的特异性收益率的波动的偏离程度越高,此时样本估计值越不靠谱,因此赋予先验的权重 vn 则越高。
基于 DolphinDB 的收益风险模型展示
如下,首先基于 getRetTable 接口得到的收益风险模型,并绘制得到的对应的模型评估指标(R2、T 统计量、Bias 统计量等)。如下绘制模型的 R_2 ,可知 12 年至 22 年模型的解释力最低为 5%,最高为 84%,平均为 37%,因此模型的解释力度较高。
// 一级因子收益率回归
retOut1 = getRetTable(facTable1,adjust = true)
// adjust采用Newey-West协方差调整、当市场收益率存在序列自相关时采用此方法
retOut1 = getRetTable(facTable1,adjust = false,shrink = false)
// shrink采用贝叶斯收缩调整特异性风险、推荐使用
retOut1 = getRetTable(facTable1,adjust = true,shrink = true)
// 特异性风险采用bayesian shrinkage
retOut1 = getRetTable(facTable1,adjust = true,shrink = true,eigenfactor = true)
// 因子风险采用eigenfactor adjust,当市场关联密切时采用此方法
retOut1 = getRetTable(facTable1,adjust = true,shrink = true,eigenfactor = true)
// 综上,推荐使用
retOut1 = getRetTable(facTable1,adjust = false,shrink = true,eigenfactor = true)
// 综上,推荐使用
retOut1 = getRetTable(facTable1,adjust = false,shrink = true,eigenfactor = true)
// 综上,推荐使用
retOut1 = getRetTable(fTable,adjust = false,shrink = true,eigenfactor = false)
// 综上,推荐使用
undef(`retOut)
retOut = getRetTable(facTable1,adjust = true,shrink = false ,eigenfactor = false)
// 综上,推荐使用
retOut1.stock_risk[string(2022.12.30)] // 12.30的特质收益协方差矩阵
retOut1.fac_risk[string(2022.12.30)] // 12.30的风险因子协方差矩阵
retOut1.R2 // R2
retOut1.res // 特质收益
retOut1.tstat // t-stat
retOut1.fac_ret // 因子收益
retOut1.bias // bias统计量
plot(retOut1.R2.stR2,retOut1.R2.record_date," R2 月频时序图")
studentized R2 月频时序图项目价值
通过DolphinDB的高性能时序处理能力,绵烁资产实现从因子挖掘、模型验证到组合优化的全流程闭环。目前,该框架已稳定支持多策略产品的日常运维,为后续人工智能因子的快速迭代奠定技术基础。